Sapparot
Oct 18, 2004
In this note, we will describe the algorithm named Sapparot. It is a pseudorandom number generator (PRNG) with good statistical characteristics and performance.
This generator consists of two 32-bit rotors with 32-bit output as a result of exclusive-OR (XOR) rotors confusion. The figure 1 below illustrates a round of Sapparot.
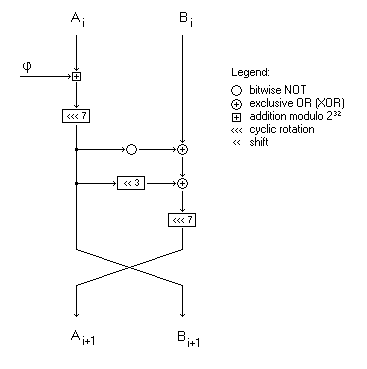
Figure 1: One round of Sapparot
Both A and B denotes rotors and φ ("phi") is a golden ratio constant. The rotors are synchronous and updates as
A = (A + φ) <<< 7 B = ( B ⊕ (¬A) ⊕ (A << 3) ) <<< 7
Rotors swap at the end of the round. The output random value is a result of (A ⊕ B). The PRNG seed is a 64-bit value that is the rotor's initial state. There are no weak seed values known for Sapparot at this moment.
Here is the portable C implementation of Sapparot:
unsigned long Sapparot(void)
{
static unsigned long a = 0, b = 0;
a += 0x9e3779b9; a = (a << 7) | (a >> 25);
b ^= (~a) ^ (a <<3 ); b = (b << 7) | (b >> 25);
b ^= a; a ^= b; b ^= a;
return (a^b);
} /* Sapparot */
The test vectors (hexadecimal values):
A = 0, B = 0 C95E78D3 1040CEB8 E65845CE 5D4283D0 5B0C7C04 030FC74F 8B15AAFD BCDAF4EE A = FFFFFFFF, B = FFFFFFFF 36A3C7AC 0485B0EF 1772A301 E4B98B3D 45FACCBD A747749E EE0D23AB 02EF9BE9 A = 9E3779B9, B = 12345678 88958DAE E5BCAF84 A91FDAD0 50667BB5 0A4F5CB0 DEF039B0 F21A594B 1799BECA
About the name: "Sapparot" is the transliteration of "pineapple" in Thai. Thai is because of few years I spent there and a pineapple… well, there is already Rambutan as a cipher so why not be a pineapple as a PRNG.
Updated on Feb 1, 2005
Despite good statistical characteristics, Sapparot is cryptographically insecure primitive as pointed by David Wagner:
"Consider the t=32 version. Let (A,B) be one state value, and (A',B') be the next state value (without swap), so that
A' = (A + phi) <<< 7 B' = (B ^ not(A') ^ (A' << 3)) <<< 7The two corresponding words of keystream output reveal D = A^B and D' = A'^B'.
Naïve attack: Guess A, use D to deduce B, calculate resulting A',B', identify correct guess using equation D' = A'^B'. Then can deduce all other keystream outputs. Workload (of this naïve attack): 2^t work.
There are better attacks that can solve the above two equations for A,B,A',B' given D,D' with O(2^10) (t=32) or O(2^18) (t=64) work, and perhaps even faster if one is more clever still."